As somebody interested in all things spatial, I was delighted that the community corner at SQLBits8 featured an interactive mapping application. Many people commented on how much work had obviously gone into the user interface: the ability to add “pushpins” was particularly realistic, and the base dataset, despite being centred on the UK, was designed to be modular and extendable – with users adding in further layers for Italy, Germany, Holland, Sweden, Norway, Denmark, Austria and Australia.
If you’re wondering, the application front-end interface in question looked like this: (red pins are usergroup locations, blue pins are attendees)
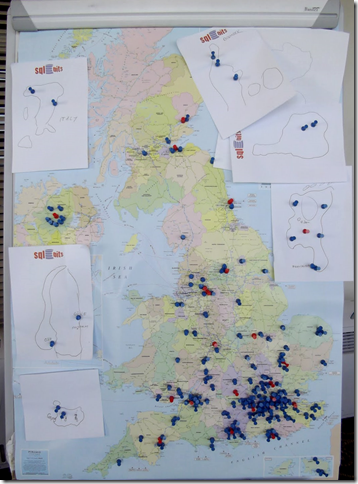
The purpose of the map was obviously both to visualise the geographic distribution of attendees coming to SQLBits, as well as to show people the location of their closest usergroup. Seeing as this was a SQL Server conference, it gave me an idea on how you could analyse this information with SQL Server spatial…
Displaying Locations of UK SQL Server Usergroups
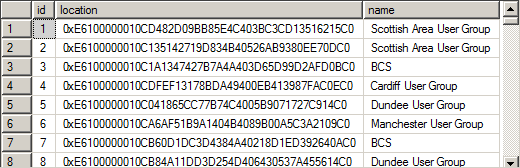
To start with, we can create a table with geography points representing regional SQL Server usergroups in the UK (information kindly provided by tsqltidy).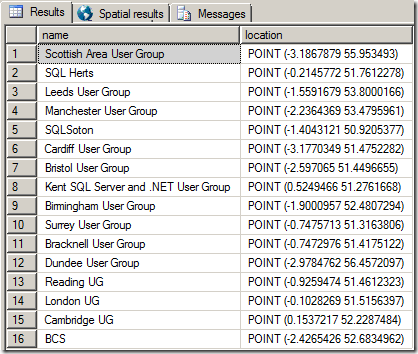
To show the locations where each usergroup is held, we can then simply select each point, buffer them by a reasonable amount (10,000m, in this case), and display them against a background map of Great Britain.
SELECT name, location.STBuffer(10000) FROM SQLServerUGs;
Here’s what the results of that query look like in the SSMS Spatial Results tab:
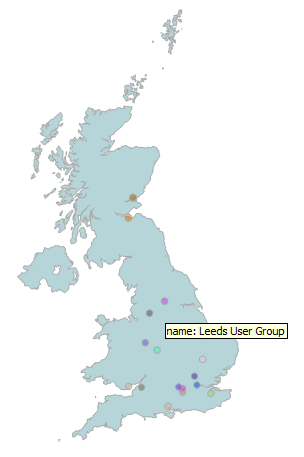
That’s the objective of visualising the locations of all UK usergroups completed…. now, what about the other purpose of the map – to let users located their closest usergroup. This is commonly known as a “nearest-neighbour” query. So how would we go about doing this?
Nearest-Neighbour Queries
I don’t know the actual locations of all the attendees of SQLBits, and I can’t be bothered to trace their locations from the little blue pins in the first photo of this post, so let’s create some dummy data instead. The following code will create a table containing the locations of 800 fictional attendees, all situated somewhere on GB mainland (maybe there are some SQL Server DBAs out in the North Sea on oil rigs or pirate ships, but let’s just assume not for the sake of simplicity):CREATE TABLE #SQLBitsAttendees (
id int identity(1,1),
location geography
);
SET NOCOUNT ON;
DECLARE @i int = 0;
WHILE @i < 800 BEGIN
DECLARE @p geography;
SET @p = geography::Point(RAND()*10+50, RAND()*8-6, 4326);
IF (@p.STIntersects(@GB)=1)
BEGIN
INSERT INTO #SQLBitsAttendees(location) VALUES (@p)
SET @i = @i + 1;
END
END
And here they all are (including a fictional attendee from the Shetland Islands, from the looks of it):
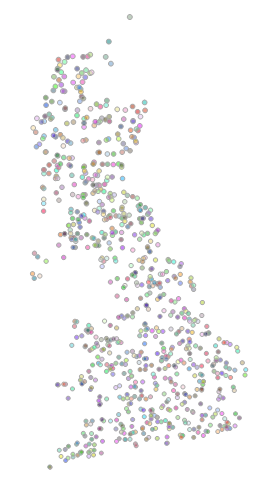
Now, to find out the location of the closest usergroup for each attendee, you could use the STDistance() method to measure and sort the distance from each usergroup, then select the TOP 1 closest in a subselect, as follows:
SELECT
id,
location,
(SELECT TOP 1 name
FROM #SQLServerUGs ug
ORDER BY ug.location.STDistance(a.location)
) AS nearestUG
FROM #SQLBitsAttendees a
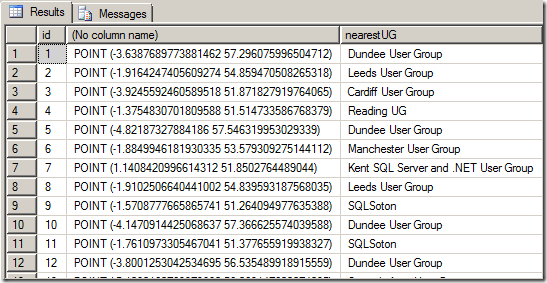
The problem with this approach is that, in order to determine the closest usergroup, the subselect statement has to evaluate the distance from every usergroup, only to select the top one. What’s more, in SQL Server 2008/R2 this query cannot take advantage of an index (spatial or otherwise), so it involves a full scan of the usergroups table for every attendee. Not good.
In SQL Server Denali, there’s a new nearest-neighbour query plan that does allow the query optimiser to use a spatial index for these types of queries, so long as they are expressed using a particular pattern. To use the nearest-neighbour plan in SQL Server Denali for this example, we have to add a IS NOT NULL condition to the STDistance() method, as follows:
SELECT
id,
location,
(SELECT TOP 1 name
FROM #SQLServerUGs ug
WHERE ug.location.STDistance(a.location) IS NOT NULL
ORDER BY ug.location.STDistance(a.location)
) AS nearestUG
FROM #SQLBitsAttendees a
This improves the performance significantly, but it’s still not an ideal query design.
One alternative approach could be to place a constraint on the subselect query, by assuming that nobody wants to travel more than 100km to attend a usergroup:
SELECT
id,
location.STAsText(),
(SELECT TOP 1 name
FROM #SQLServerUGs ug
WHERE ug.location.STDistance(a.location) < 100000
ORDER BY ug.location.STDistance(a.location)
) AS nearestUG
FROM #SQLBitsAttendees a
The advantage of this approach is that a spatial index can be used to fulfil the STDistance()query predicate (in both SQL Server 2008 and Denali), so this can efficiently reduce the number of rows that need to be evaluated and sorted. An added benefit is that it also allows us to identify all those users who are further than 100km from their closest usergroup, since the subselect will return NULL for those records:
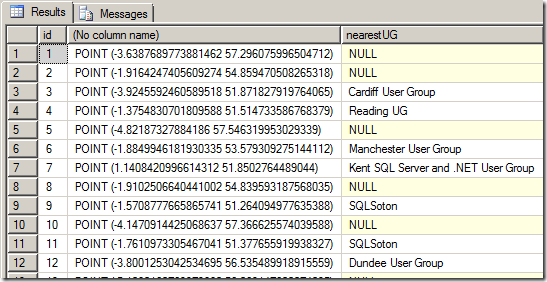
(Perhaps users with a NULL nearestUG should consider starting their own local group?)
This approach is still not perfect though, since it relies on a fairly arbitrary limit of 100km for the limit within which to search. Setting this limit too high and we leave ourselves with a lot of data still to sort. But set it too low and some keen DBAs and Devs might be willing to travel further than the specified limit, and would miss out on knowing what their closest UG would be.
Another alternative solution, first proposed by Isaac Kunen, is to make use of a numbers table to create a query that looks for nearest neighbours in an expanding series of search ranges. The initial search area is set small, but then expands exponentially outwards until a neighbour is found. A query using this logic looks something like this:
DECLARE @start FLOAT = 1000;
WITH NearestUGs AS
(
SELECT TOP(1) WITH TIES *, T.g.STDistance(@x) AS dist
FROM Numbers JOIN T WITH(INDEX(spatial_index))
ON T.g.STDistance(@x) < @start*POWER(2,Numbers.n)
ORDER BY n
)
SELECT TOP(1) * FROM NearestUGs
ORDER BY n, dist
(for explanation of what’s going on here, I suggest you refer to Isaac’s post).
Empirically, this query works pretty well – but it’s not exactly pretty to look at and it’s pretty daunting unless you’re proficient with fairly advanced T-SQL as well as with the nuisances of dealing with spatial data. So, there’s still scope for a better solution.
Enter Voronoi diagrams…
Voronoi Diagrams
A Voronoi diagram is a formed from a set of underlying points (called Voronoi sites). Around each site is a Voronoi cell, which is the area made up of all those points that lie closest to that site than to any other site. The edges at which two Voronoi cells meet is therefore constructed from all those points that lie equidistant between the two sites.The complete set of Voronoi cells form a tessellating, non-overlapping set of of Polygons that cover the full extent of a set of data, known as a Voronoi tessellation.
Voronoi diagrams are closely related to Delauney triangulations (which I also used in my post about alpha shapes). In fact, if you connect the circumcenters of all the triangles in a Delauney triangulation, you’ll create a Voronoi tessellation of the original set of points, as shown below:
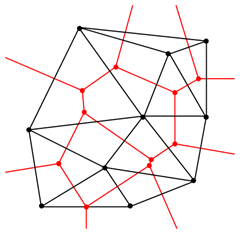
Delauney triangulation (black lines) and Voronoi tessellation (red lines) of a set of points. Image from http://en.wikipedia.org/wiki/File:Delaunay_Voronoi.png
The simplest (although not necessarily the most efficient) way to construct the Voronoi tessellation of a set of points is to take advantage of this duality. First, create the Delauney triangulation of the points, and then connect the circumcenters of all those triangles that have a common vertex to create the Voronoi cell around the site at that vertex. You can find more details on the algorithms required to create Delauney Triangulations and Voronoi tessellations at http://www.cs.cmu.edu/~quake/triangle.html and http://paulbourke.net/papers/triangulate/, as well as plenty of other resources on the internet. You know where to look.
What’s all this got to do with nearest neighbour queries? Well, suppose we create a Voronoi tessellation based on the set of points representing the location of SQL Server UGs. The result will be a set of (convex) polygons, in which each polygon contains exactly one usergroup, and all those points closest to that usergroup than to any other. If we store each Voronoi cell as a geography Polygon and clip them to the outline map of Great Britain, we get something a bit like this:
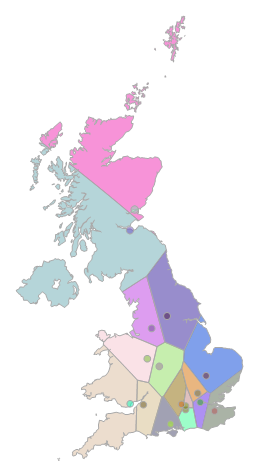
You can think of the coloured polygons as representing the “catchment area” for each of the usergroups. In order to work out the closest usergroup for any attendee, all we therefore have to do is to work out which polygon their location lies in, which can be done with a simple STIntersects() query:
SELECT
a.id,
a.location,
ug.name AS nearestUG
FROM #SQLBitsAttendees a
JOIN SQLServerUGs ug ON a.location.STIntersects(ug.area) = 1
And here they all are, assigned to the correct UG, and much quicker than any of the preceding queries (as the STIntersects() predicate is fully capable of taking advantage of any spatial index):
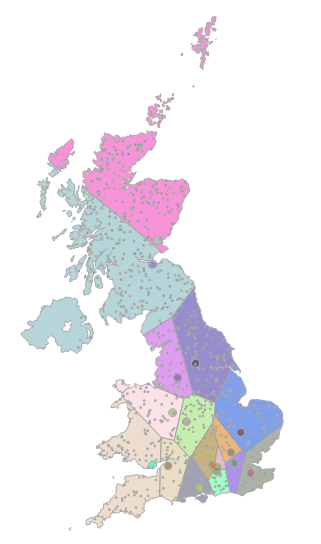
The only thing to remember is that you will have to recreate the underlying Voronoi tessellation every time the distribution of usergroups changes (i.e. every time a usergroup is added/removed/or starts meeting at a new location). However, we can probably safely assume that new usergroups don’t pop up every day, and it doesn’t take that long to recreate the tessellation anyway. For nearest-neighbour queries where the “neighbours” are relatively static, Voronoi tessellations are therefore a very good choice.
You can download the code used in the examples above from here.
No comments:
Post a Comment